Published online: 24.06.2019
Author: James M. Byrne
So you have managed to get access to a Mössbauer spectrometer and measured a sample, but then you realise that it needs to be calibrated! Or maybe you have already calibrated and want to know how to do it? In this tutorial I will down break the fundamentals behind calibrating a sample and explain what really happens when you press the magic "calibrate" button in your fitting software. I have broken this section into small steps including:
If you have read up about, or attended a few workshops on Mössbauer spectroscopy you probably learned that there is a maximum of 6 peaks in a Mössbauer spectrum due to hyperfine splitting of the ground and excited states. But now as you stare at your very first dataset you see 12!! This is no mistake, and the cause is relatively easy to understand. Since the radioactive source moves forwards and backwards, the typical Mössbauer spectrum develops with two symmetrical halves because half the time the radiation is moving towards your sample, and half the time it is moving away.
The real challenge is in trying to covert these 12 peaks into just 6 so that you can start fitting and analysing your data. To make life easier, let’s just consider our calibration. Calibration is usually done with a metallic foil such as alpha-Fe(0), although in former times other materials were used. Hopefully you have already done a calibration using your spectrometer, but if not then download one:
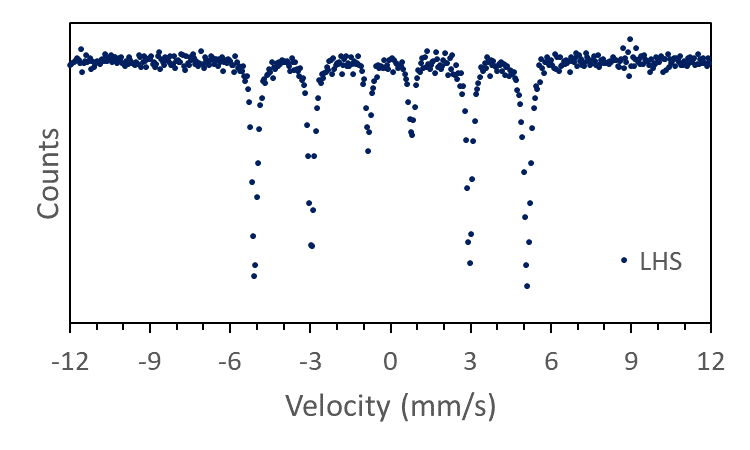
If you open your raw unprocessed data in Notepad, Excel, Origin, Matlab or whatever your tool of choice, you will see a list of numbers. These correspond to the data or "Counts". Each value corresponds to the value that has been binned into a separate channel. In the data I provided, there are 1024 values, corresponding to the 1024 channels used during the measurement. If you plot the Count data (Excel usually just makes up an ascending x-axis when you do not specify one) you will obtain a spectrum similar to Figure 1. The x-axis is simply an ascending set of numbers from 1 to 1024 corresponding to the measurement channel. You can also clearly see 12 main peaks. If you consider an imaginary line at about channel 500, you can clearly see a cluster of 6 lines on the left, and 6 lines on the right. These are symmetrical versions of the same spectrum and arise because of the back and forth motion of the source. From now on, I will refer to these clusters as the left hand side (LHS) and right hand side (RHS).
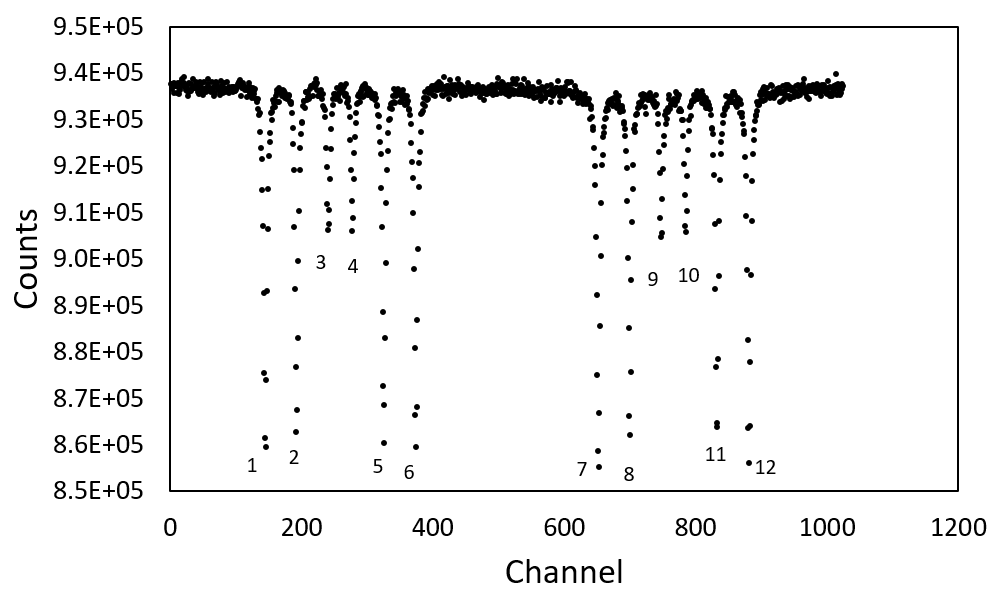
Having a list of channel number for an x-axis is not so helpful to us because it means our spectrum cannot be compared to reference spectra, or to any data collected on a different spectrometer. This is because we have not calibrated the foil to a velocity yet, however, luckily each of the 12 peaks in the calibration foil has a defined velocity (Table 1), so in principle all we need to do is find the channels corresponding to the peak, and do a simple conversion to velocity.
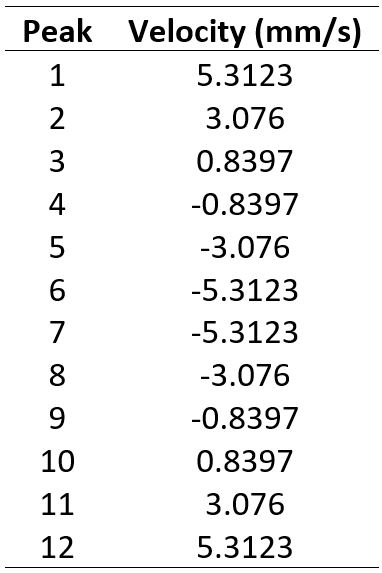
You should spot that each velocity is listed twice, i.e. Peak 1 and 12 both have a velocity of 5.3123 mm/s. This goes back to the symmetry of the spectrum, and the fact that the source is moving back and forth. This also means that when properly calibrated, we should be able to fold our spectrum over on itself and double our signal to noise ratio. But how do we actually do this calibration and folding?
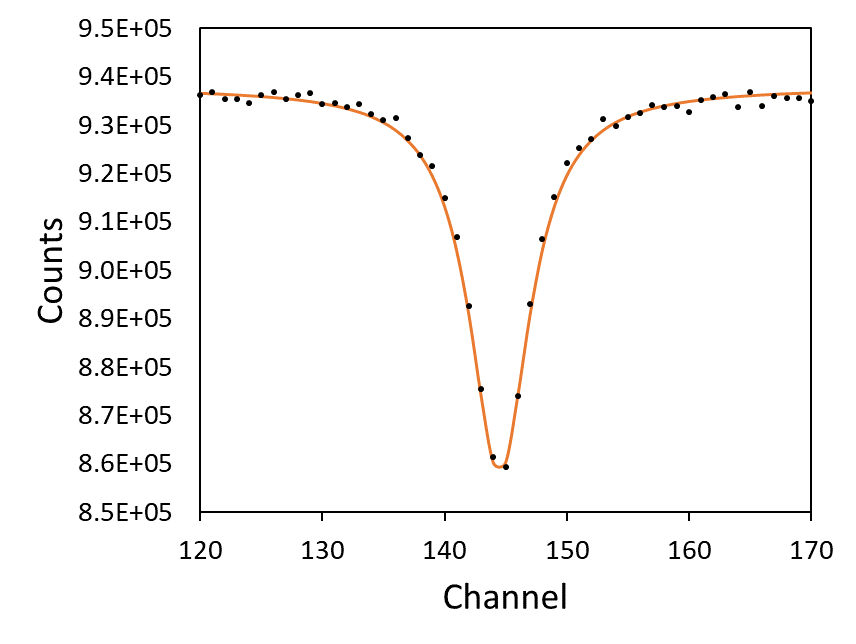
The first step in our folding procedure is to find the channel corresponding to each peak in Figure 1, i.e. determine the exact channel number which corresponds to each peak 1-12. If you do this by eye, you only get an integer number, which will lead to inaccuracies in your calibration. The correct method is to fit a Lorentzian line function to each peak and then use the centre of these peaks as your true peak channel (Figure 2).
Once you have the channel numbers for each peak, you can assign the channel number to the actual velocity listed (See tables 2 and 3). At this stage, it is also a good idea to divide your results into the left hand side (LHS) and the right hand side (RHS):
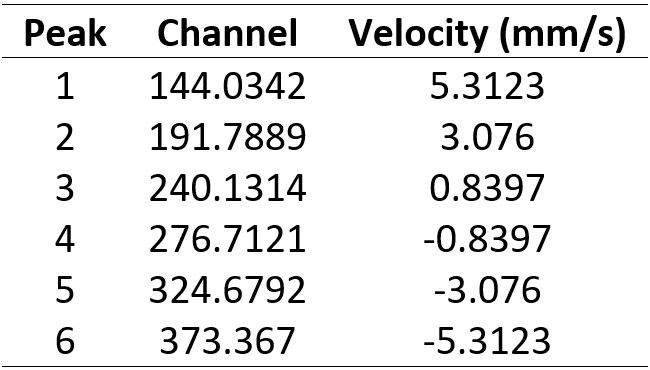
If you plot curves showing Channel vs. Velocity for both the LHS and RHS. You should see two straight lines, one with a positive gradient and one with a negative gradient (Figure 3). Fit a straight line to each dataset and find the coefficients (i.e. gradient and y-intercept).
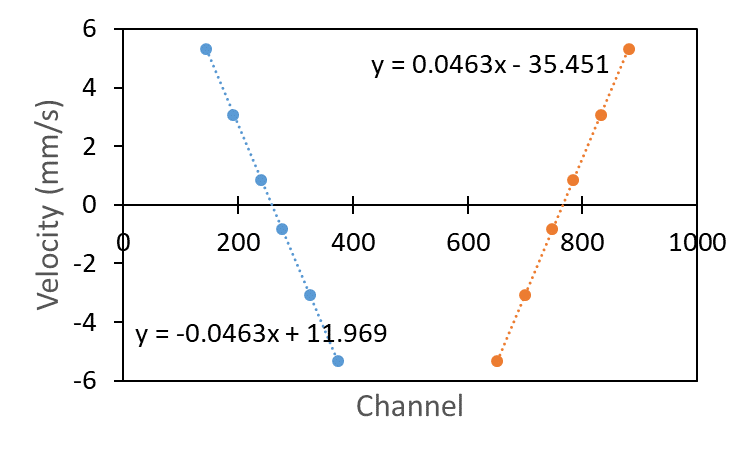
LHS: Velocity = -0.0463 * Channel + 11.969
RHS: Velocity = 0.0463 * Channel - 35.451
We now have two expressions which we can use to calibrate our data. To do this, split your calibration spectrum into two parts corresponding to the LHS and RHS. If you have collected your data over 1024 channels, you can simply take the top 512 values and the bottom 512 values. Arrange your data so that for both LHS and RHS you have a column for channel number, an empty column for velocity, and a column for Counts (Table 4).
Now using the equations for the LHS and RHS, fill in the velocity column (Table 5).
If you were to plot the curves you would now see two, almost identical overlapping curves consisting of six lines (Figure 4).
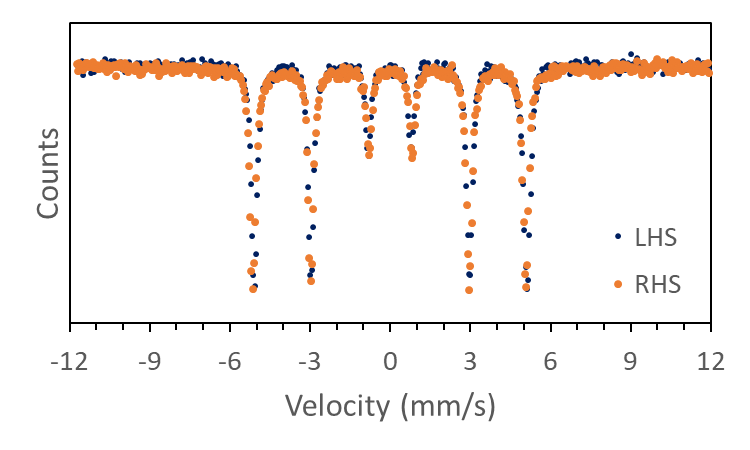
Great, does that mean we can just add the LHS and RHS up and be done with it? ...nice try, but no!
The problem we have now is that the velocity of the LHS and the RHS are slightly different from each other. The difference is very minor, and you might think it is not a big deal but you first would need to consider which velocity axis you should use for your data and what to do with the very minor shifts in velocity, all of which contribute to a slight broadening of your data and therefore increase inaccuracy of fitting.
We can overcome this issue by interpolating your data. Interpolation is a useful trick that can be used to essentially draw a new x-axis with defined range and step size, and which can be accurately applied to both your LHS and RHS data (read up about linear interpolation online). There are tools available in Matlab which can help you to interpolate your data, but since we want to go to basics, let's try and do it with Excel!
Linear interpolation allows you to estimate x and x for any point not explicitly provided in your data set, or essentially fill in the gaps. Linear interpolation uses the equation below, where y corresponds to our "counts" and x corresponds to "velocity":
$$y = y_1 + (x-x_1){(y_2 - y_1) \over (x_2 - x_1)}$$
The method assumes that any change in y for a given x is linear. This only works if the data points are very close together, which for us is true. If you lowered the number of channels to e.g. 256, then this approximation would be less accurate, though still probably acceptable.
To do this in Excel, we need to use the MATCH and INDEX functions. MATCH returns the location of a value (n) in a column or row of data, whereas INDEX returns the actual value in the nth position. They are relatively easy to understand, but in case you have never heard of them before then I advise you to check them out online.
Actually using MATCH and INDEX can get a bit tricky so I have broken it down into some steps which you can follow directly:
Make sure you fill down all of the columns across the full velocity range and there you have it! You now have completed the data interpolation for the LHS data. Your spreadsheet should look something like Table 6. Pretty easy wasn't it?
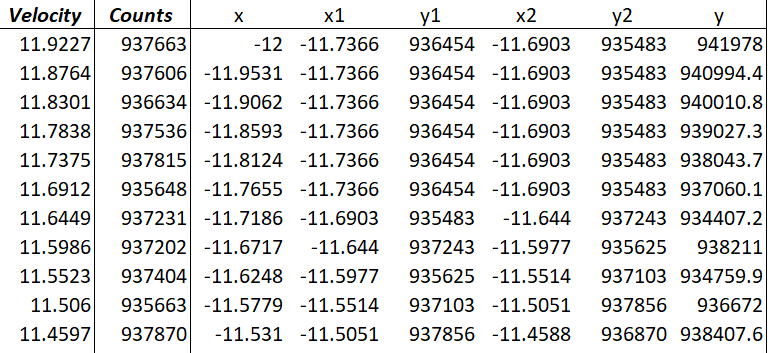
If you plot x against y, you should get the classic Mössbauer spectrum we are hoping for (Figure 5).
What about the RHS? It is more or less the same, however you should see that your data starts at -12 rather than +12 as was the case for the LHS. Because of this, we need some minor adjustments to our formula. At this stage, I advise creating a new workbook called RHS, and using the steps above, interpolate the RHS but note the minor changes in the formula:
x1: =INDEX(A$2:A$513;MATCH(C2;A$2:A$513;1))
y1: =INDEX(B$2:B$513;MATCH(C2;A$2:A$513;1))
x2: =INDEX(A$2:A$513;MATCH(C2;A$2:A$513;1)+1)
y2: =INDEX(B$2:B$513;MATCH(C2;A$2:A$513;1)+1)
Don't be worried about any "#N/A" results you obtain. These occur because we have relatively arbitrarily decided to split our data into two halves with exactly equal number of entries. Some programs have a way to overcome this, however it does not affect our results too much.
Once you have completed the interpolation for both LHS and RHS, you should have count data which fit along the same velocity axis. We can see this by creating a new workbook called "SUM", and copying in the column for "x" which is our new velocity, and also the "y" columns for both the LHS and RHS data. Create a new column which sums up the LHS and RHS count data using the formula:
=B2 + C2
This new column is our calibrated, folded and most accurate count data. Use this for all of your fitting and data analysis needs.
The great thing about this method, is that you can use it to manually fold your own spectra obtained from real samples, not just the calibration. All you need to do, is start at the section "Calibrate the left and the right" with your own data and continue along the rest of the tutorial. Here is an example spectrum you can try it with:
This might seem to be a long winded way of calibrating and folding data, and when you use a standard fitting program this is all achieved in a matter of seconds. However, hopefully you now have a better understanding about what happens when you calibrate your spectrum. Furthermore, you should also realise why it is so important that you calibrate frequently, and always keep a good record about what calibration file is associated with the data collected for any sample you might collect a spectrum for.
Finally, if you have not understand something or are having a hard time making it work, then just download my Excel spreadsheet which contains all of the information described above:
Did you like this tutorial? Is there anything which can be improved? Or perhaps you want to contribute you own tutorial? If so, please get in touch.